A bank’s Rates desk has purchased a callable fixed rate bond. The embedded call means the bond’s issuer is long a call option on interest rates, and the bank is short one. If rates fall, the issuer will call the bond, and the bank will not gain the upside of the bond’s high fixed rate. A payer swaption is economically equivalent to the embedded call. The bank purchases a payer swaption so that the loss in value of the bond when rates fall – due to the embedded call – will be offset by an increase in the value of the swaption. The terms of the swaption gives the bank the right to enter a fixed-for-floating swap on the same date as the call date of the bond.
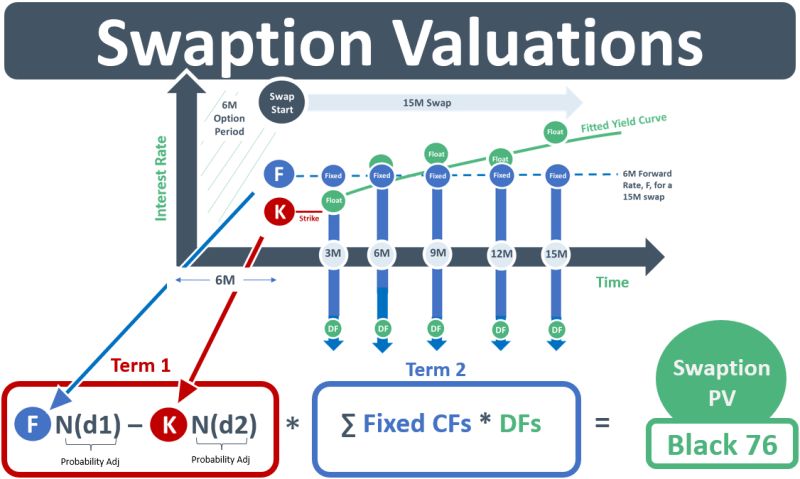
In the diagram above, if the swaption is exercised, the CFs of the swap will start in 6M. They are determined using the diff btw the swap’s fixed rate and its floating rate. The floating rate is taken from a published OIS rate index that is based on overnight rates compounded daily over the prior 3-month period. The net CFs are multiplied by DFs obtained from a RF yc. The bank has constructed its yc using rates from a series OIS swaps observable at different maturities. The curve is made smooth and continuous using a bootstrapping routine with interpolation.
However, the Rates desk is not valuing a swap, it is valuing a swaption. The swap valuation procedure above needs to be adjusted for the fact that the swap will only occur if rates fall below the strike rate. The swap is therefore a forward starting swap that is contingent upon the forward rate falling to a certain strike level. The bank has chosen the Black 76 model to value the swaption. Its core modelling assumption is that it only cares about the fixed CFs of the swap. It doesn’t care about the floating CFs. This is because the swap will be a par swap, i.e., the PV of floating CFs will equal the PV of the fixed CFs, meaning the swap will have a value of par on the forward start date if the option is exercised. The PV the fixed CFs is shown as Term 2 in the diagram.
Because the forward starting swap is contingent upon rates falling below the strike level, the PV of its fixed CFs need to be adjusted for the probability that rates will fall that far. This probability adjustment is shown in Term 1 in the diagram.
If rates do fall that far then the value of the swaption at the end of the option period will be equal to the amount that the forward rate F falls below the strike level K, i.e., F minus K. During the option period, therefore, the value of the swaption will be [F minus K] adjusted for the probability that rates fall that much. The Black 76 model assumes that this probability is obtained from a lognormal distribution of forward swap rates. The model is an adaption, tailored for interest rate options, of the seminal Black-Scholes-Merton option pricing model which was focused on equity options. Black 76 was developed by Fisher Black, one of the authors of the original BSM model, in 1976.