If you are lucky enough to get 100% interest on an investment of $1 over 1 yr, you will get back $2. If int is compounded semi-annually, you will get back $2.25. If int is compounded quarterly, you will get $2.44. Infinite compounding gives you $2.718. 2.718 is the number e. It is called after Leonhard Euler, the most prolific mathematician that ever lived. It is one of the four most important numbers in the world. The others are 0, 1 and π.
In 1748 Euler published the Euler identity. It linked e to the other three numbers: 0 minus 1 equals e to the power of π (multiplied by i). The first two numbers, 0 and 1 exist in the discrete world. They do not exist in the natural world. The number 1 implies that two of the same thing can exist. But in the natural world that does not happen. No two things are identical and there are infinitely many non-discrete numbers btw 1 and 2.
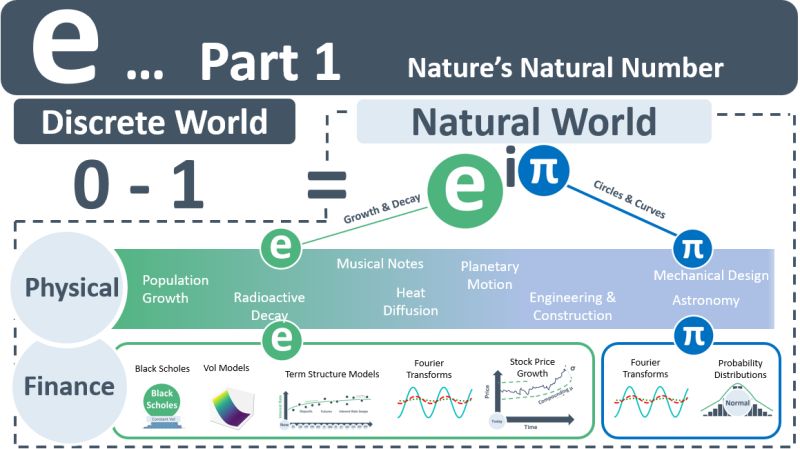
e and π are the numbers that allow phenomenon in the natural world to be modelled.
e is used to model the growth or decay of physical phenomenon. π is a number that allows us to move from theoretical straight-line geometry to the naturally occurring world of curvature. When converted into multiples of the discrete number 1, π equals the non-discrete number 3.142. It is the ratio of a straight-line to the circumference of the most famous of all curves, the circle.
In the physical world, e captures rates of change for population, radioactivity, heat, and harmonic motion. In finance, it models the growth and decay of investments. In both cases, the rate of change is modelled over continuous time. In nature there are no discrete time intervals – there is only continuous time.
In finance, a future cash flow is decayed using e to arrive at a present value. This fundamental concept leads to the ubiquitous use of e in investment & risk. It appears in stock price growth, Black-Scholes option pricing, term structure models, volatility models, market & credit risk, and several PDFs. Plotting financial variables such as stock prices against time is modelled with functions [ f(t) = ]. A central objective of quantitative finance is the analysis of the curves (usually non π-related) that result from these functions. This analysis requires the use of calculus. The calculus of growth and decay functions in finance is made easier by one of the amazing natural facts about the number e: its derivative is equal to itself.
While the number π appears less frequently in finance than it does in the physical world, it does appear in probability distributions, Fourier Series, and other quant finance techniques that are based on waves and repeating curvature and circular-like motions. In the physical world, on the other hand, where the geometry of lines, circles & curves plays a central role, π appears everywhere.