This week’s note is about the central role that market data plays in the no-arbitrage valuation paradigm that emerged to price complex IR derivatives.
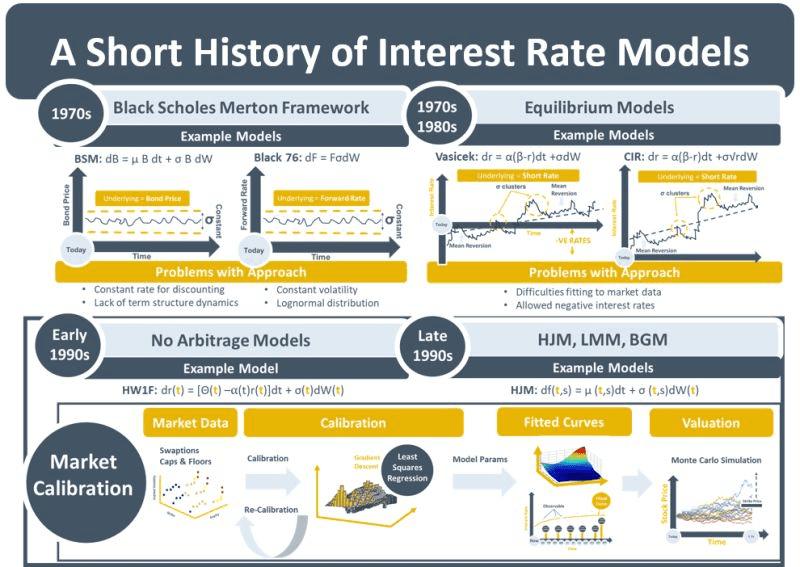
When demand for complex IR derivatives increased in the 1980s and 90s, new IR models were required, triggering innovation. The no-arbitrage valuation framework that exists today results from this period. It requires traders and valuations teams to regularly re-calibrate model parameters to market data. While this has the benefit of market consistency, the approach has circular and self-re-enforcing characteristics.
The first IR models were based on the BSM model. Assumptions of a single, constant discount rate were incorrect as were assumptions that bond prices were lognormal and had constant volatility. While the Black 1976 model helped with the constant vol problem, it lacked a mechanism for incorporating the term structure of interest rates. The first term structure models were equilibrium models. Model parameters were specified using assumptions about interest rate behaviour derived from empirical observation. The no-arbitrage models that succeeded them, on the other hand, calibrated those model parameters to observable market data.
No-arbitrage pricing and the calibration process was a paradigm shift. It ensured that curves would always automatically fit the market consensus – with little incentive to challenge the consensus. By choosing the no-arbitrage approach over the equilibrium approach, the derivatives industry was implicitly deciding that market quotes for benchmark instruments contained more information about the behaviour of the term structure than available historical data.
The emergence of complex IR derivatives that contained vega and other risks led to traders needing to find market prices for multiple offsetting hedging trades. This accelerated the no-arbitrage transformation as in parallel it made sense for model parameters to be calibrated to the same instruments that were used for hedging. The BSM-calculated prices for caps, floors and swaptions had a new purpose: they became the hedging instruments for complex derivatives and the benchmarking instruments for model calibration.
As derivative valuation frameworks evolved, they did so around the no-arbitrage paradigm. The HJM and LMM models emerged to model and calibrate the entire term structure. With everybody calibrating to everyone else and regulators enforcing punitive model reserves and market risk capital on banks that did not match market prices, there was little incentive to revert to the historical data analysis used in the original equilibrium models.
It took financial crises of different sorts for models to be adjusted. Adjacent modelling paradigms emerged to address the market dislocations that created phenomena such as volatility smiles and the multi-curve framework.