In some of the market data projects we have been working on recently, FX volatilities is one of the quote instrument types that has come up. This prompted me to write this note.
A call option is the right to buy something … shares, bonds, gold bars … it could be anything. But what if you had the right to buy money? Well, that is what an FX option is … it is the right to buy an amount of one currency, i.e., money, using another currency.
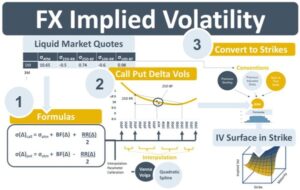
This differentiating feature of FX options has led to quoting conventions that are complex compared to those of EQ, CO and IR options. With FX options, for example, premiums can be paid in either currency and option prices can be quoted in foreign or domestic notional or pips of that notional. The option’s risk measure, delta, is central to the quoting process. The quote can be based on spot delta or forward delta and the delta calculation needs to be aware of whether the premium is paid in domestic or foreign currency. In addition, market-makers quote option prices using trading strategies called risk reversals (RR) and butterflies (BF) that combine prices of call and put options and quote them in FX implied volatilities (IVs) and IV spreads at 25 and 10-delta moneyness.
To abstract from this quoting convention complexity, a series of transformations are needed to generate an IV surface in strike and maturity dimension that looks similar to the surfaces of other options products. The resulting surface will be used for subsequent valuation and risk-management tasks.
The transformation process converts the ATM, 25D & 10D RR and BF quotes available on the broker market data feed into a calculated IV surface. Broadly, it has 3 steps. The first step transforms the 25 & 10D RR and BF quotes into call and put IVs of the same deltas. It does this for all maturities on the surface. The transformation is done with straightforward arithmetic. The second step is the calculation of call and put IVs for the full delta-smile, i.e., IVs at deltas other than 10D and 25D. This can be done using interpolation methods such as Vanna Volga or the appropriate spline method. The third step is the conversion of the interpolated call & put IV smiles from smiles containing delta IVs to ones containing strike IVs. This is done using a series of formulas based on the Black-Scholes-Merton (BSM) model that factors in the quoting conventions of the input RR, BF, and ATM quotes.